With an explosive growth of the internet, data need to be localized more than ever. Many DBMS already include some GIS features but support is often incomplete. InnoDB’s MySQL engine currently supports some spacial data types but not indexes on it. Building an efficient GIS system from scratch is quite easy, let’s see how to do it using Ruby on Rails & MySQL.
The distances between two points on a sphere from their longitudes and latitudes can be calulated using the Haversine formula (half-versed-sine). Because the earth is not a perfect sphere but an oblate spheroid, this formula gives an approximated distance with a margin of error generally below 0.3% (the earth radius varies from 6356.752 km at the poles to 6378.137 km at the equator). For a greater accuracy, the Vincenty’s formula could be used.
Because we are using high-precision floating point numbers, we are able to use the simpler Spherical law of cosines formula : d = acos(sin(φ1).sin(φ2) + cos(φ1).cos(φ2).cos(Δλ)).R where φ is latitude, λ is longitude.
The first thing to do is to implement the Spherical law of cosines formula in a MySQL function to be able to use it easily into queries.
The earth radius can be chosen depending on where you want to make those calculations. Miles can also be used instead of kilometers.
1 2 3 4 5 6 7 8 9 | |
So if we consider that we have a table point_of_interests including 2 fields lat (latitude) and lng (longitude), a way to find all POIs in a 50 km radius around a given point 48.852842, 2.350333 could be :
1 2 | |
The big performance issue with this query is that it does a whole table scan to calculate distance between the point and all POIs. It can be ok if you have few POIs but in most cases it sucks hard.
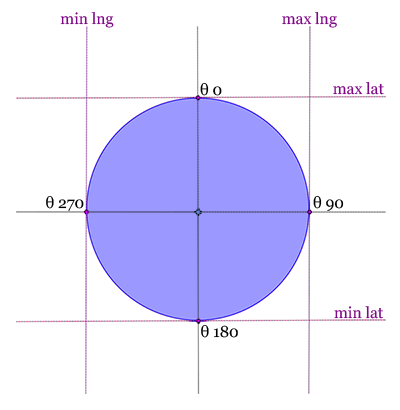 To limit the number of records to scan, we need to find the latitude and longitude boundaries where all POIs we are looking for are included.
To limit the number of records to scan, we need to find the latitude and longitude boundaries where all POIs we are looking for are included.
These boundaries are illustrated on the schema and are located at 4 differents bearings and obviously at a radius distance.
- θ 0 : Maximum latitude
- θ 90 : Maximum longitude
- θ 180 : Minimum latitude
- θ 270 : Minimum longitude
Using the Haversine formula, we are able to find geographic coordinates of a point with another point, a bearing and the distance between the two points.
Latitude φ2 = asin(sin(φ1)*cos(d/R) + cos(φ1)*sin(d/R)*cos(θ))
Longitude λ2 = λ1 + atan2(sin(θ)*sin(d/R)*cos(φ1), cos(d/R)−sin(φ1)*sin(φ2))
where φ is latitude, λ is longitude, θ is the bearing (in radians, clockwise from north), d is the distance, R is the earth’s radius (d/R is the angular distance, in radians).
To be able to add the distance search feature to any Active Record models, the search code can be included into a Concern.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | |
Just include the Localizable concern into each models you need to (off course the corresponding table must have lat & lng fields).
1 2 3 4 5 | |
You’re done !
1 2 3 | |